My research focuses on modelling the dynamics of ecological systems, from both theoretical (study of prey-predator or host-parasitoid systems) and more applied (forest, epidemic, fishery) perspectives. I use methods coming from the mathematical (dynamical systems) and computer (cellular automata network, individual-based models) sides of ecological modelling. Since 2003 I am employed by the Institut de Recherche pour le Développement (IRD) and presently in the MARBEC research unit.
Marine dispersal and connectivity
I am currently coordinating the GDRI-Sud iMarCo, a research group funded by the IRD on marine connectivity. This research group constitutes the African component of the international GDRI iMarCo group. It gathers researchers and PhD students from several African countries (Algeria, Cote d'Ivoire, Djibouti, Mozambique, Senegal, South Africa, Tunisia) with various scientific expertise in genetics, otolithometry, and modelling. From 2010 to 2015 I led the COMPO research project on marine population connectivity in New Caledonia. Before this I was involved in the French - South African co-operation research program IDYLE , that evolved into ECO-UP, a joint program between the IRD and other institutions, mainly University of Cape Town (UCT) and Marine & Coastal Management (MCM) in South Africa, Instituto del Mar del Perú (IMARPE) in Peru and Institut National de Recherche Halieutique (INRH) in Morocco. These programs focused on studying the structure and functioning of exploited upwelling ecosystems. I was in charge of developing models to study how physical (e.g., currents, water temperature) and biological (e.g., growth, mortality) factors affect the dispersal of ichthyoplankton (fish eggs and larvae). This activity resulted in the Ichthyop Lagrangian tool. The images below, obtained with this tool, show an example of the dispersal pattern for passive individuals released within five different areas off the South African south coast.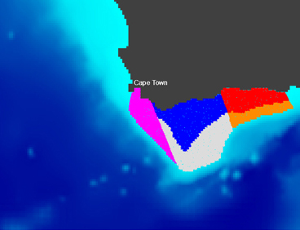
Release
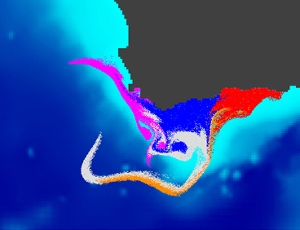
After 5 days
After 10 days
Animal groups in motion
Animal groups such as fish schools, bird flocks, insect swarms and mammal herds, have spectacular collective behaviours. Efforts in trying to formalise the basic individual behaviours responsible for animal groups complex dynamics began more than 50 years ago, and since then many models of the dynamics of animal groups have been proposed in the literature. Different approaches have been used in these models, coming from the mathematics, physics, and computer sides of science. In most individual-based models of animal groups, individuals have three types of local interactions with their neighbours, attraction, alignment and repulsion, operating mainly at long, medium and short distances, respectively. The most famous example of it is probably the Boids computer model. Another example is the Aquarium applet that I found on the Web some time ago (and could not find back, so unfortunately I am not able to acknowledge the author). If interested in such tools you can also visit Cool School.
Simulated group before an attack
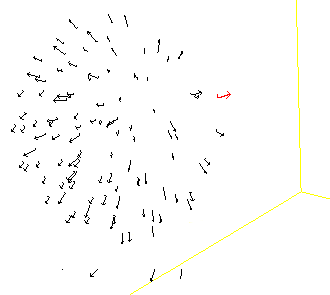
Simulated group after the attack
You can see video files (avi format)
Epidemic spread
From November 1999 to September 2000, I had a post-doctoral position at RISØ National Laboratory - Plant Biology and Biogeochemistry Department - Plant Genetics and Epidemiology Programme in Roskilde, Denmark. I developed a model simulating the spatiotemporal spread of plant disease epidemics in cultivar mixtures. The project focused on the dynamics of pathogens attacking cereal cultivars, and more specifically on the dynamics of yellow rust (Puccinia striiformis) in wheat cultivar mixtures.Example of epidemics spread simulation
Space represents a 12 m side square parcel. Initially, one infection is put in the centre of the parcel (image on the left). An infection focus forms (image in the centre), develops, and satellite foci appear (image on the right). Each black pixel represents an infected plant. Each yellow pixel is a non infected plant. On the shown example, the parcel has a density of 400 plants per hectare and there is only one cultivar.
Infection
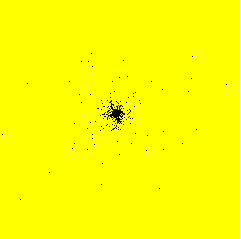
After 30 days
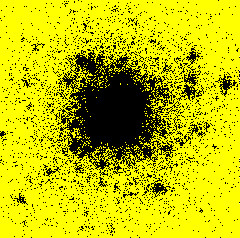
After 50 days
You can see the whole simulation in a video file (avi format 1 Mb or compressed zip format 137 Kb).
Forest dynamics
 I defended my Ph.D. thesis in Life Sciences - Ecology on the 3rd of November 1999 at University of Strasbourg, France. The work was achieved during three years in Laboratoire des Sciences de l'Image, de l'Informatique et de la Télédétection (Image Sciences, Computer Sciences and Remote Sensing Laboratory) - Groupe de Recherches en Télédétection et Spatialisation (Remote Sensing and Spatialisation Research Group), within a pluridisciplinary project associating mathematics, computer sciences and ecology.
I defended my Ph.D. thesis in Life Sciences - Ecology on the 3rd of November 1999 at University of Strasbourg, France. The work was achieved during three years in Laboratoire des Sciences de l'Image, de l'Informatique et de la Télédétection (Image Sciences, Computer Sciences and Remote Sensing Laboratory) - Groupe de Recherches en Télédétection et Spatialisation (Remote Sensing and Spatialisation Research Group), within a pluridisciplinary project associating mathematics, computer sciences and ecology.
My Ph.D. fitted into a new project aiming at developing one or several models that enable to answer questions concerning forest communities biodiversity, in particular on the factors which favour their species richness. My personal contribution to this project was to study to what extent simulation models of forest dynamics could give insights to these questions. My work showed that before using such models for prediction, there were several difficult stages to pass through: choice of the model, choice between different approaches of spatialisation, sensitivity analysis of the parameters and initial conditions, validation towards field data.
To get details about this work you can download my Ph.D. dissertation (in French, pdf file 2.8 Mb).
Example of forest dynamics simulation
The simulated forest ecosystem consists of three groups of species: shade tolerant (in green), shade intolerant (white) and intermediate (yellow) species. The tree crowns are represented by discs within a 50 m side square parcel. Starting from a situation where no individual is present, shade intolerant (light-demanding) species first install (image on the left), then intermediate species succeed (image in the centre), and shade tolerant species finally dominate while other species persist within gaps created by the death of big individuals (image on the right).
After 30 years

After 150 years

After 600 years
Mathematical and computer modelling
The different methods used to build models of population dynamics stand on a large spectrum with, on one side of the spectrum, simple mathematics-based models (using differential equations or matrices) and, on the other side of the spectrum, complex computer-based models (or simulation models, like individual-based models or multi-agent systems). The advantage of the mathematics-based models is that they may be tractable analytically, but they are often considered as over-simplifications of the reality. On the contrary, computer-based models are closer to reality but their dynamics can only be tracked through extensive simulations. There is not much interaction between these two "worlds" of population dynamics modelling. Developing such interactions was one of the objectives of the Mathematical Biology Team in Laboratoire de Biométrie et Biologie Evolutive at University of Lyon, France, in which I got an Assistant Professor position in September 2000.Example of the SIRS model
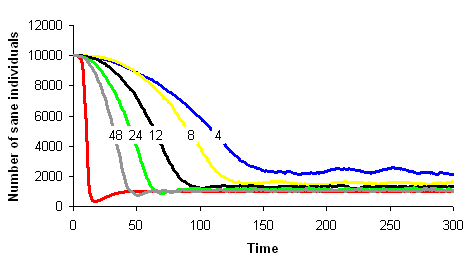
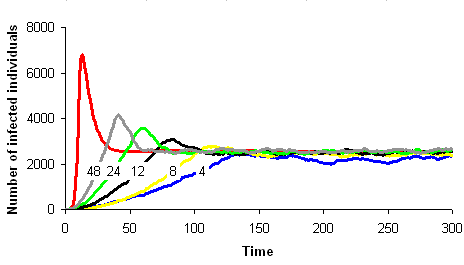
One can imagine to build a simulation model simple enough to stay close to a given mathematical model and analyse the conditions under which the two models show similar dynamics. Let's take the example of the SIRS model in epidemiology. We wish to build a spatial version of this model. We can build a computer model where space is discrete, e.g., a grid of square cells. Each cell takes one of three possible states, S (sane, in blue on the images below), I (infected, in red) or R (removed, in green). A cell in state S switches to state I the time step after with a probability equal to the proportion of cells in state I in its neighbourhood. A cell in state I switches to state R with a constant probability. Similarly, a cell in state R switches to state S with a constant probability. The model built this way is a stochastic cellular automata network. This model was implemented using the programming environment Cormas developed by Cirad. The simulation model dynamics converges to a situation where the number of cells in each state remains approximately constant, as predicted by the mathematical model.
Infection
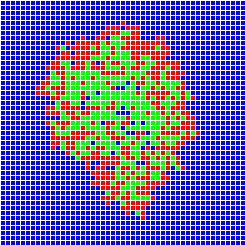
After 30 time steps

After 100 time steps
You can see the simulation in a video file (avi format 1 Mb or compressed zip format 128 Kb).
The correspondence between the mathematical model dynamics (red curve on the images below) and the computer model dynamics (blue, yellow, black, green and grey curves) improves as the neighbourhood size increases (4, 8, 12, 24 et 48 neighbours on the images below).
Host-parasitoid and prey-predator systems
Host-parasitoid
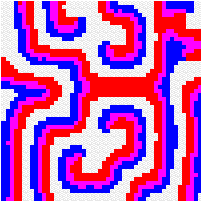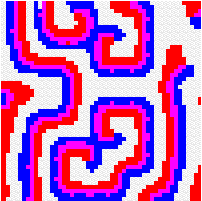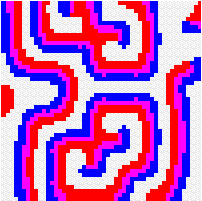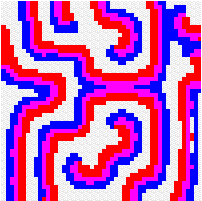 Another way to build the gap between mathematics-based and computer-based models may be to build mathematical models that take more into account individual behaviour than classical models do. This has a cost, the difficulty to get analytical results concerning the resulting complex models. Variables aggregation method is often useful to reduce the dimension of such models, in the case where they involve processes which take place at different temporal scales, for example migratory processes at a fast time scale (daily, weekly) and demographic processes at a slow time scale (monthly, yearly). We adopted this method to reconsider classical host-parasitoid models (like the Nicholson-Bailey model) in a spatial context, with individual migrating from one patch to a neighbouring patch several times within a generation before the parasitism interaction takes place. This study showed that migration, when it is asymmetrical (the parasitoids, principally, should move in a preferred direction), could facilitate the persistence of host-parasitoid interactions. Other studies (Hassell et al. 1991; Comins et al. 1992) suggested that local migration could stabilise host-parasitoid interactions through the emergence of spatiotemporal patterns like spirals (the animation in the margin) or spatial chaos.
Another way to build the gap between mathematics-based and computer-based models may be to build mathematical models that take more into account individual behaviour than classical models do. This has a cost, the difficulty to get analytical results concerning the resulting complex models. Variables aggregation method is often useful to reduce the dimension of such models, in the case where they involve processes which take place at different temporal scales, for example migratory processes at a fast time scale (daily, weekly) and demographic processes at a slow time scale (monthly, yearly). We adopted this method to reconsider classical host-parasitoid models (like the Nicholson-Bailey model) in a spatial context, with individual migrating from one patch to a neighbouring patch several times within a generation before the parasitism interaction takes place. This study showed that migration, when it is asymmetrical (the parasitoids, principally, should move in a preferred direction), could facilitate the persistence of host-parasitoid interactions. Other studies (Hassell et al. 1991; Comins et al. 1992) suggested that local migration could stabilise host-parasitoid interactions through the emergence of spatiotemporal patterns like spirals (the animation in the margin) or spatial chaos.
Prey-predator

 A lot of studies have addressed the potential benefits and costs of group living for predators and for prey, but this has not been much formalised within a model. We focused on the "many eyes - many mouths trade-off", assuming a trade-off between the benefits of group living (increased predation efficiency for predators, increased defence against predation for prey) and the costs (the need to share the captured prey for the predators, to share the resources for the prey). We built a model based on game theory to study this trade-off. The model results are in accordance with empirical evidence that habitat openness encourages group living, and that low risks of predation favour lonely prey. Under some conditions, complex dynamics may occur, like time oscillating proportions of grouped predators and prey.
A lot of studies have addressed the potential benefits and costs of group living for predators and for prey, but this has not been much formalised within a model. We focused on the "many eyes - many mouths trade-off", assuming a trade-off between the benefits of group living (increased predation efficiency for predators, increased defence against predation for prey) and the costs (the need to share the captured prey for the predators, to share the resources for the prey). We built a model based on game theory to study this trade-off. The model results are in accordance with empirical evidence that habitat openness encourages group living, and that low risks of predation favour lonely prey. Under some conditions, complex dynamics may occur, like time oscillating proportions of grouped predators and prey.
Publications
Articles
[70] Giachini Tosetto E, Lett C, Koch-Larrouy A, Costa da Silva A, Neumann-Leitão S, Nogueira Junior M, Barrier N, Dossa AN, Tchilibou M, Bauchot P, Morvan G, Bertrand A (2024). Identifying community-based recruitment zones and connectivity pathways in the Tropical Southwestern Atlantic Ocean. Ecography 2024(3): e0711.
[69] Barrier C, Ternengo S, El Idrissi O, Piacentini L, Barrier N, Lett C, Pasqualini V, Durieux EDH (2024). Edible sea urchin (Paracentrotus lividus) larval dispersal and connectivity modelling in the northwestern Mediterranean Sea. Journal of Sea Research 197: 102464.
[68] Lett C, Malauene BS, Hoareau T, Kaplan DM, Porri F (2024). Corridors and barriers to marine connectivity around southern Africa. Marine Ecology Progress Series 731: 105–127.
[67] Muller C, Lett C, Porri F, Pattrick P, Bailey D, Denis H, Barrier N, Potts W, Kaplan DM (2024). Coastal connectivity of an abundant inshore fish species: model-data comparison along the southern coast of South Africa. Marine Ecology Progress Series 731: 89–104.
[66] Flores-Valiente J, Lett C, Colas F, Pecquerie L, Aguirre-Velarde A, Rioual F, Tam J, Bertrand A, Ayón P, Sall S, Barrier N, Brochier T (2023). Influence of combined temperature and food availability on Peruvian anchovy (Engraulis ringens) early life stages in the northern Humboldt Current system: A modelling approach. Progress in Oceanography 215: 103034.
[65] Imzilen T, Kaplan DM, Barrier N, Lett C (2023). Simulations of drifting fish aggregating device (dFAD) trajectories in the Atlantic and Indian Oceans. Fisheries Research 264: 106711.
[64] Podlejski W, Berline L, Nerini D, Doglioli A, Lett C (2023). A new Sargassum drift model derived from features tracking in MODIS images. Marine Pollution Bulletin 188: 114629.
[63] Podlejski W, Descloitres J, Chevalier C, Minghelli A, Lett C, Berline L (2022). Filtering out false Sargassum detections using context features. Frontiers in Marine Science 9: 960939.
[62] MacMillan I, Attrill MJ, Imzilen T, Lett C, Walmsley S, Chu C, Kaplan DM (2022). Spatio-temporal variability in drifting Fish Aggregating Device (dFAD) beaching events in the Seychelles Archipelago. ICES Journal of Marine Science 79(5): 1685–1700.
[61] Imzilen T, Lett C, Chassot E, Maufroy A, Goujon M, Kaplan DM (2022). Recovery at sea of abandoned, lost or discarded drifting fish aggregating devices. Nature Sustainability 5: 593–602. Nature Research Highlight
[60] Dupaix A, Capello M, Lett C, Andrello M, Barrier N, Viennois G, Dagorn L (2021). Surface habitat modification through industrial tuna fishery practices. ICES Journal of Marine Science 78(9): 3075–3088.
[59] Malauene BS, Lett C, Marsac F, Roberts MJ, Brito A, Abdula S, Moloney CL (2021). Spawning areas of two shallow-water penaeid shrimps (Penaeus indicus and Metapenaeus monoceros) on the Sofala Bank, Mozambique. Estuarine, Coastal and Shelf Science 253: 107268.
[58] Imzilen T, Lett C, Chassot E, Kaplan DM (2021). Spatial management can significantly reduce dFAD beachings in Indian and Atlantic Ocean tropical tuna purse seine fisheries. Biological Conservation 254: 108939.
[57] Bonnin L, Lett C, Dagorn L, Filmalter JD, Forget F, Verley P, Capello M (2021). Can drifting objects drive the movements of a vulnerable pelagic shark? Aquatic Conservation: Marine and Freshwater Ecosystems 31(1): 74–82.
[56] Amemou H, Koné V, Aman A, Lett C (2020). Assessment of a Lagrangian model using trajectories of oceanographic drifters and fishing devices in the Tropical Atlantic Ocean. Progress in Oceanography 188: 102426.
[55] Crochelet E, Barrier N, Andrello M, Marsac F, Spadone A, Lett C (2020). Connectivity between seamounts and coastal ecosystems in the Southwestern Indian Ocean. Deep-Sea Research Part II 176: 104774.
[54] Stelfox M, Lett C, Reid G, Souch G, Sweet M (2020). Minimum drift times infer trajectories of ghost nets found in the Maldives. Marine Pollution Bulletin 154: 111037.
[53] Lett C, Barrier N, Bahlali M (2020). Converging approaches for modeling the dispersal of propagules in air and sea. Ecological Modelling 415: 108858.
[52] Lagarde F, Fiandrino A, Ubertini M, Roque d’orbcastel E, Mortreux S, Chiantella C, Bec B, Bonnet D, Roques C, Bernard I, Richard M, Guyondet T, Pouvreau S, Lett C (2019). Duality of trophic supply and hydrodynamic connectivity drives spatial patterns of Pacific oyster recruitment. Marine Ecology Progress Series 632: 81–100.
[51] Lett C, Barrier N, Ourmières Y, Petit C, Labonne M, Bourjea J, Darnaude AM (2019). Modeling larval dispersal for the gilthead seabream in the northwestern Mediterranean Sea. Marine Environmental Research 152: 104781.
[50] Imzilen T, Chassot E, Barde J, Demarcq H, Maufroy A, Roa-Pascuali L, Ternon J-F, Lett C (2019). Fish aggregating devices drift like oceanographic drifters in the near-surface currents of the Atlantic and Indian Oceans. Progress in Oceanography 171: 108–127.
[49] Flores-Valiente J, Tam J, Brochier T, Colas F, Pecquerie L, Aguirre-Velarde A, Mendo J, Lett C (2019). Larval supply of Peruvian scallop to the marine reserve of Lobos de Tierra Island: a modeling approach. Journal of Sea Research 144: 142–155.
[48] Malauene BS, Moloney CL, Lett C, Roberts MJ, Marsac F, Penven P (2018). Impact of offshore eddies on shelf circulation and river plumes of the Sofala Bank, Mozambique Channel. Journal of Marine Systems 185: 1–12.
[47] Santos AMP, Nieblas AE, Verley P, Machado A, Bonhommeau S, Lett C, Garrido S, Peliz A (2018). Sardine (Sardina pilchardus) larval dispersal in the Iberian upwelling system, using coupled biophysical techniques. Progress in Oceanography 162: 83–97.
[46] Calò A, Lett C, Mourre B, Pérez-Ruzafa Á, García-Charton JA (2018). Use of Lagrangian simulations to hindcast the geographical position of propagule release zones in a Mediterranean coastal fish. Marine Environmental Research 134: 16–27.
[45] Lagarde F, Roque d’orbcastel E, Ubertini M, Mortreux S, Bernard I, Fiandrino A, Chiantella C, Bec B, Roques C, Bonnet D, Miron G, Richard M, Pouvreau S, Lett C (2017). Recruitment of the Pacific oyster Crassostrea gigas in a shellfish-exploited Mediterranean lagoon: discovery, driving factors and a favorable environmental window. Marine Ecology Progress Series 578: 1–17. (Feature Article).
[44] Kaplan DM, Cuif M, Fauvelot C, Vigliola L, Nguyen-Huu T, Tiavouane J, Lett C (2017). Uncertainty in empirical estimates of marine larval connectivity. ICES Journal of Marine Science 74(6): 1723–1734.
[43] Koné V, Lett C, Penven P, Bourlès B, Djakouré S (2017). A biophysical model of S. aurita early life history in the northern Gulf of Guinea. Progress in Oceanography 151: 83–96.
[42] Kirkman SP, Bianchi G, Blamey L, Field JG, Huggett JA, Hutchings L, Jackson-Veitch J, Jarre A, Lamont T, Lett C, Lipinski M, Mafwila SW, Pfaff MC, Samaai T, Shannon LJ, Shin Y-J, van der Lingen CD, Yemane D (2016). Spatial characterisation of the Benguela ecosystem for ecosystem based management. African Journal of Marine Science 38(1): 7–22.
[41] Garavelli L, Colas F, Verley P, Kaplan DM, Yannicelli B, Lett C (2016). Influence of biological factors on connectivity patterns for Concholepas concholepas (loco) in Chile. PLoS ONE 11(1): e0146418.
[40] Thiebault A, Semeria M, Lett C, Tremblay Y (2016). How to capture fish in a school? Effect of successive predator attacks on seabird feeding success. Journal of Animal Ecology: 85(1): 157–167.
[39] Lett C, van der Lingen CD, Loveday BR, Moloney CL (2015). Biophysical models of larval dispersal in the Benguela Current ecosystem. African Journal of Marine Science 37(4): 457–465.
[38] Cuif M, Kaplan DM, Fauvelot C, Lett C, Vigliola L (2015). Monthly variability of self-recruitment for a coral reef damselfish. Coral Reefs 34(3): 759–770.
[37] Lett C, Nguyen-Huu T, Cuif M, Saenz-Agudelo P, Kaplan DM (2015). Linking local retention, self-recruitment, and persistence in marine metapopulations. Ecology 96(8): 2236–2244.
[36] Cuif M, Keller F, Chateau O, Kaplan DM, Labonne M, Lett C, Vigliola L (2014). Evaluation of transgenerational isotope labeling of embryonic otoliths in a coral reef damselfish with single and repeated injections of enriched 137Barium. Journal of Experimental Marine Biology and Ecology 459: 151–159.
[35] Lett C, Semeria M, Thiebault A, Tremblay Y (2014). Effects of successive predator attacks on prey aggregations. Theoretical Ecology 7(3): 239–252.
[34] Garavelli L, Kaplan DM, Colas F, Stotz W, Yannicelli B, Lett C (2014). Identifying appropriate spatial scales for marine conservation and management using a larval dispersal model: the case of Concholepas concholepas (loco) in Chile. Progress in Oceanography 124: 42–53.
[33] Cuif M, Kaplan DM, Lefèvre J, Faure VM, Caillaud M, Verley P, Vigliola L, Lett C (2014). Wind-induced variability in larval retention in a coral reef system: a biophysical modelling study in the South-West Lagoon of New Caledonia. Progress in Oceanography 122: 105–115.
[32] Martins RS, Roberts MJ, Lett C, Chang N, Moloney CL, Camargo MG, Vidal EAG (2014). Modelling transport of chokka squid (Loligo reynaudii) paralarvae off South Africa: reviewing, testing and extending the Westward Transport Hypothesis. Fisheries Oceanography 23(2): 116–131.
[31] Koné V, Lett C, Fréon P (2013). Modelling the effect of food availability on recruitment success of Cape anchovy ichthyoplankton in the southern Benguela upwelling system. African Journal of Marine Science 35(2): 151–161.
[30] Grüss A, Kaplan DM, Lett C (2012). Estimating local settler-recruit relationship parameters for complex spatially explicit models. Fisheries Research 127–128: 34–39.
[29] Garavelli L, Grüss A, Grote B, Chang N, Smith M, Verley P, Stenevik EK, Kaplan DM, Lett C (2012). Modeling the dispersal of Cape hake ichthyoplankton. Journal of Plankton Research 34(8): 655–669.
[28] Moussaoui A, Auger P, Lett C (2011). Optimal number of sites in multi-site fisheries with fish stock dependent migrations. Mathematical Biosciences and Engineering 8(3): 769–783.
[27] Brochier T, Mason E, Moyano M, Berraho A, Colas F, Sangrà P, Hernández-León S , Ettahiri O, Lett C (2011). Ichthyoplankton transport from the African coast to the Canary Islands. Journal of Marine Systems 87(2): 109–122.
[26] Brochier T, Lett C, Fréon P (2011). Investigating the 'northern Humboldt paradox' from model comparisons of small pelagic fish reproductive strategies in eastern boundary upwelling ecosystems. Fish and Fisheries 12(1): 94–109.
[25] Lett C, Ayata S-D, Huret M, Irisson J-O (2010). Biophysical modelling to investigate the effects of climate change on marine population dispersal and connectivity. Progress in Oceanography 87(1–4): 106–113.
[24] Kaplan DM, Planes S, Fauvelot C, Brochier T, Lett C, Bodin N, Le Loc'h F, Tremblay Y, Georges J-Y (2010). New tools for the spatial management of living marine resources. Current Opinion in Environmental Sustainability 2(1–2): 88–93.
[23] Auger P, Lett C, Moussaoui A, Pioch S (2010). Optimal number of sites in artificial pelagic multisite fisheries. Canadian Journal of Fisheries and Aquatic Sciences 67(2): 296–303.
[22] Brochier T, Colas F, Lett C, Echevin V, Cubillos LA, Tam J, Chlaida M, Mullon C, Fréon P (2009). Small pelagic fish reproductive strategies in upwelling systems: a natal homing evolutionary model to study environmental constraints. Progress in Oceanography 83(1–4): 261–269.
[21] Brochier T, Lett C, Tam J, Fréon P, Colas F, Ayón P (2008). An individual-based model study of anchovy early life history in the northern Humboldt Current system. Progress in Oceanography 79(2–4): 313–325.
[20] Mirabet V, Fréon P, Lett C (2008). Factors affecting information transfer from knowledgeable to naive individuals in groups. Behavioral Ecology and Sociobiology 63(2): 159–171.
[19] Brochier T, Ramzi A, Lett C, Machu E, Berraho A, Fréon P, Hernández-León S (2008). Modelling sardine and anchovy ichthyoplankton transport in the Canary Current System. Journal of Plankton Research 30(10): 1133–1146.
[18] Lett C, Mirabet V (2008). Modelling the dynamics of animal groups in motion. South African Journal of Science 104(5–6): 192–198.
[17] Lett C, Verley P, Mullon C, Parada C, Brochier T, Penven P, Blanke B (2008). A Lagrangian tool for modelling ichthyoplankton dynamics. Environmental Modelling & Software 23(9): 1210–1214.
[16] Nguyen-Huu T, Auger P, Lett C, Marvà M (2008). Emergence of global behaviour in a host-parasitoid model with density-dependent dispersal in a chain of patches. Ecological Complexity 5(1): 9–21.
[15] Lett C, Veitch J, van der Lingen CD, Hutchings L (2007). Assessment of an environmental barrier to transport of ichthyoplankton from the southern to the northern Benguela ecosystems. Marine Ecology Progress Series 347: 247–259.
[14] Lett C, Penven P, Ayón P, Fréon P (2007). Enrichment, concentration and retention processes in relation to anchovy (Engraulis ringens) eggs and larvae distributions in the northern Humboldt upwelling ecosystem. Journal of Marine Systems 64(1–4): 189–200.
[13] Mirabet V, Auger P, Lett C (2007). Spatial structures in simulations of animal grouping. Ecological Modelling 201(3–4): 468–476.
[12] Lett C, Roy C, Levasseur A, van der Lingen CD, Mullon C (2006). Simulation and quantification of enrichment and retention processes in the southern Benguela upwelling ecosystem. Fisheries Oceanography 15(5): 363–372.
[11] Mchich R, Auger P, Lett C (2006). Effects of aggregative and solitary individual behaviors on the dynamics of predator-prey game models. Ecological Modelling 197(3–4): 281–289.
[10] Miller DCM, Moloney CL, van der Lingen CD, Lett C, Mullon C, Field JG (2006). Modelling the effects of physical-biological interactions and spatial variability in spawning and nursery areas on transport and retention of sardine Sardinops sagax eggs and larvae in the southern Benguela ecosystem. Journal of Marine Systems 61(3–4): 212–229.
[9] Nguyen-Huu T, Lett C, Auger P, Poggiale J-C (2006). Spatial synchrony in host-parasitoid models using aggregation of variables. Mathematical Biosciences 203(2): 204–221.
[8] Nguyen-Huu T, Lett C, Poggiale J-C, Auger P (2006). Effect of movement frequency on global host-parasitoid spatial dynamics with unstable local dynamics. Ecological Modelling 197(3–4): 290–295.
[7] Lett C, Auger P, Fleury F (2005). Effects of asymmetric dispersal and environmental gradients on the stability of host-parasitoid systems. Oikos 109(3): 603–613.
[6] Lett C, Auger P, Gaillard J-M (2004). Continuous cycling of grouped vs. solitary strategy frequencies in a predator-prey model. Theoretical Population Biology 65(3): 263–270.
[5] Auger P, Lett C (2003). Integrative biology: linking levels of organization. Comptes Rendus Biologies 326(5): 517–522.
[4] Lett C, Auger P, Bravo de la Parra R (2003). Migration frequency and the persistence of host-parasitoid interactions. Journal of Theoretical Biology 221(4): 639–654.
[3] Lett C, Silber C, Barret N (1999). Comparison of a cellular automata network and an individual-based model for the simulation of forest dynamics. Ecological Modelling 121(2–3): 277–293.
[2] Lett C, Silber C, Dubé P, Walter J-M, Raffy M (1999). Forest dynamics: a spatial gap model simulated on a cellular automata network. Canadian Journal of Remote Sensing 25(4): 403–411.
[1] Lett C, Walter J-M (1999). Validation of an individual-based model of forest dynamics using self-thinning relationships. Comptes Rendus de l’Académie des Sciences - Sciences de la Vie 322(10): 879–885.
Books and chapters




[5] Auger P, Lett C, Poggiale J-C (2015). Modélisation mathématique en écologie, cours et exercices corrigés, 2e édition. Dunod Sciences Sup.
[4] Cury P, Bertrand A, Bertrand S, Lett C, Weigel J-Y, Masski H, Andréfouët S (2015). Chapitre 6. Océans : les écosystèmes marins face au réchauffement. In : Reinert M, Janicot S, Aubertin C, Bernoux M, Dounias E, Guégan J-F, Lebel T, Mazurek H, Sultan B, Sokona Y, Moatti J-P (eds), Changement climatique : quels défis pour le Sud ?, IRD éditions, pp. 87–99.
[3] Auger P, Lett C, Poggiale J-C (2010). Modélisation mathématique en écologie, cours et exercices corrigés. Dunod Sciences Sup.
[2] Lett C, Rose KA, Megrey BA (2009). Chapter 6. Biophysical models. In: Checkley DM, Alheit J, Oozeki Y, Roy C (eds), Climate change and small pelagic fish, Cambridge University Press, pp. 88–111.
[1] Auger P, Lett C, Nguyen-Huu T (2009). Aggregation methods of time discrete models: review and application to host-parasitoid interactions. In: Abdulle A, Banasiak J, Damlamian A, Sango M (eds), Multiple scales problems in Biomathematics, Mechanics, Physics and Numerics, Gakuto International Series in Mathematical Sciences and Applications, Vol. 31, pp. 257–278.
Ph.D. dissertations
[12] Imzilen T (2021) (partly in French). Analyse et modélisation des trajectoires des dispositifs à concentration de poissons dérivants (DCP) dans les zones océaniques tropicales et estimation des risques associés à leur déploiement. Sorbonne Université. Graduation ceremony[11] Amemou H (2021) (partly in French). Modélisation biophysique de la dispersion et de la croissance des larves de sardinelles dans le Golfe de Guinée. Sorbonne Université and Université Félix Houphouët-Boigny, Abidjan, Ivory Coast.
[10] Lagarde F (2018) (partly in French, pdf file 2 Mb). Écologie de la reproduction de l’huître Crassostrea gigas en lagune méditerranéenne. Sorbonne Université. Overview
[9] Malauene BS (2015) (pdf file 46 Mb). Environmental influences on banana shrimps of the Sofala Bank, Mozambique Channel. University of Cape Town, South Africa.
[8] Cuif M (2014) (partly in French, pdf file 9 Mb). Combinaison de la modélisation biophysique et de marquages isotopiques pour estimer la connectivité démographique des populations marines : application à Dascyllus aruanus dans le lagon sud-ouest de Nouvelle-Calédonie. Université Pierre et Marie Curie.
[7] Garavelli L (2013) (partly in French, pdf file 6 Mb). Étude de la connectivité larvaire pour la gestion des ressources marines : application au gastéropode Concholepas concholepas ("loco") au Chili. Université Pierre et Marie Curie and Universidad Católica del Norte, Coquimbo, Chile.
[6] Martins RS (2009) (pdf file 3 Mb). Some factors influencing the transport of chokka squid (Loligo reynaudii d'Orbigny, 1839) paralarvae off the Eastern Cape, South Africa. University of Cape Town, South Africa.
[5] Brochier T (2009) (partly in French, pdf file 9 Mb). Stratégie de reproduction des petits poissons pélagiques dans les zones d’upwelling : une approche par modélisation individu-centrée appliquée aux systèmes de courants de Humboldt et des Canaries. Université Paris VI.
[4] Mirabet V (2007) (in French, pdf file 5 Mb). Modélisation individu-centrée de la dynamique des groupes d'animaux et applications aux bancs de poissons. Université Lyon I.
[3] Koné V (2006) (in French, pdf file 10.9 Mb). Modélisation de la production primaire et secondaire de l’écosystème du Benguela sud. Influence des conditions trophiques sur le recrutement des larves d’anchois. Université Paris VI.
[2] Miller DCM (2006) (pdf file 4 Mb). An individual-based modelling approach to examine life history strategies of sardine (Sardinops sagax) in the southern Benguela ecosystem. University of Cape Town, South Africa.
[1] Lett C (1999) (in French, pdf file 2.8 Mb). Modélisation et simulation de la dynamique des écosystèmes forestiers : des modèles agrégés aux modèles individuels spatialisés. Université Strasbourg I.
Contact
